Q-1: Classify the following numbers as rational or irrational:
(i) $2-\sqrt{5}$
(ii) $(3 +\sqrt{23})- \sqrt{23}$
(iii) $\cfrac{2\sqrt{7}}{7\sqrt{7}}$
(iv) $\cfrac{1}{\sqrt{2}}$
(v) $2\pi$
Solution:
(i) $2-\sqrt{5}$
Here, 2.2360679…is non-terminating and non-recurring.
$\therefore 2-\sqrt{5} = 2-2.2360679… = -0.2360679$
Since the number, – 0.2360679…, is non-terminating non-recurring, 2 –√5 is an irrational number.
(ii) $(3 +\sqrt{23})- \sqrt{23}$
$(3 +\sqrt{23} –\sqrt{23} = 3+\sqrt{23}–\sqrt{23} = 3 = \cfrac{3}{1}$
$\because$ $(3 +\sqrt{23})- \sqrt{23} = \cfrac{3}{1}$ which is of the form $\cfrac{p}{q}$.
$\therefore (3 +\sqrt{23})- \sqrt{23}$ is a rational number.
(iii) $\cfrac{2\sqrt{7}}{7\sqrt{7}}$
$\cfrac{2\sqrt{7}}{7\sqrt{7}} = \cfrac{2}{7}$
Since $\cfrac{2}{7}$ is in $\cfrac{p}{q}$ form, $\cfrac{2\sqrt{7}}{7\sqrt{7}}$ is rational.
(iv) $\cfrac{1}{\sqrt{2}}$
$\cfrac{1}{\sqrt{2}}\times\cfrac{\sqrt{2}}{\sqrt{2}} = \cfrac{\sqrt{2}}{2} = \cfrac{1.4142…}{2} = 0.7071..$
Since the number, $0.7071..$ is non-terminating non-recurring, $\cfrac{1}{\sqrt{2}}$ is an irrational number.
(v) $2\pi$
We know, $\pi = 3.1415…$
$\therefore 2\pi = 2\times3.1415… = 6.2830…$
Since, $6.2830…$, is non-terminating and non-recurring, $2\pi$ is an irrational number.
Q-2: Simplify each of the following expressions:
(i) $(3+\sqrt{3})(2+\sqrt{2})$
(ii) $(3+\sqrt{3})(3-\sqrt{3})$
(iii) $(\sqrt{5}+\sqrt{2})^2$
(iv) $(\sqrt{5}-\sqrt{2})(\sqrt{5}+\sqrt{2})$
Solution:
(i) $(3+\sqrt{3})(2+\sqrt{2})$
= $3(2+\sqrt{2}) + \sqrt{3}(2+\sqrt{2})$
= $6 + 3\sqrt{2} + 2\sqrt{3} + \sqrt{6}$
(ii) $(3+\sqrt{3})(3-\sqrt{3})$
= $3^2 – (\sqrt{3})^2$
= $9-3 = 6$
(iii) $(\sqrt{5}+\sqrt{2})^2$
= $(\sqrt{5})^2 + (\sqrt{2})^2 + 2\sqrt{5}\sqrt{2}$
= $5 + 2 + 2\sqrt{10}$
= $7 + 2\sqrt{10}$
(iv) $(\sqrt{5}-\sqrt{2})(\sqrt{5}+\sqrt{2})$
= $(\sqrt{5})^2 – (\sqrt{2})^2$
= $5-2 = 3$
Q-3: Recall, $\pi$ is defined as the ratio of the circumference (say c) of a circle to its diameter, (say d). That is, $\pi =\cfrac{c}{d}$. This seems to contradict the fact that $\pi$ is irrational. How will you resolve this contradiction?
Solution:
We can never determine an exact value using tools like scales. As a result, we can’t definitively say whether a measured value is rational or irrational. While $\pi$ is often approximated as $\cfrac{22}{7}$ or 3.142857, these are just close estimates of its true, irrational value.
$\therefore$ There’s no contradiction here.
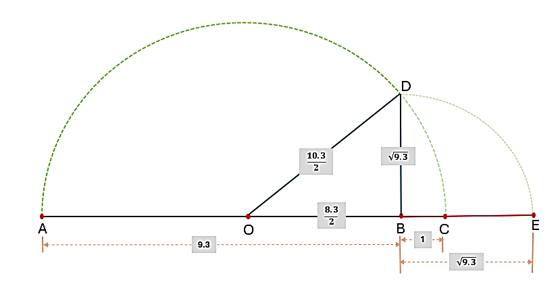
Q-4: Represent $(\sqrt{9.3})$ on the number line.
Solution:
Step 1: Draw a line segment AB of length 9.3 units. Extend AB by 1 unit to point C.
Step 2: Find the midpoint O of line segment AC.
Step 3: Construct a semicircle with center O and radius OC.
Step 4: Draw a perpendicular line to AC at point B, intersecting the semicircle at point D.
Step 5: Triangle OBD is a right-angled triangle with a right angle at B.
- Using the Pythagorean Theorem:
- $OD = OC = \cfrac{10.3}{2}$ (radius of the semicircle)
- $OB = OC – BC = (\cfrac{10.3}{2}) – 1 = \cfrac{8.3}{2}$
- $OD^2 = BD^2 + OB^2$
- $(\cfrac{10.3}{2})^2 = BD^2 + (\cfrac{8.3}{2})^2$
- $BD^2 = (\cfrac{10.3}{2})^2 – (\cfrac{8.3}{2})^2$
- $BD^2 = 9.3$
- $BD = \sqrt{9.3}$
Step 6: With center B and radius BD (which is $\sqrt{9.3}$ units), draw an arc intersecting line segment AC. The point of intersection is at a distance of $\sqrt{9.3}$ units from point O.
Q-5: Rationalize the denominators of the following:
(i) $\cfrac{1}{\sqrt{7}}$
(ii) $\cfrac{1}{(\sqrt{7} – \sqrt{6})}$
(iii) $\cfrac{1}{(\sqrt{5} + \sqrt{2})}$
(iv) $\cfrac{1}{(\sqrt{7} – 2)}$
Solutions:
(i) $\cfrac{1}{\sqrt{7}}$
= $\cfrac{1}{\sqrt{7}}\times\cfrac{\sqrt{7}}{\sqrt{7}} = \cfrac{\sqrt{7}}{7}$
(ii) $\cfrac{1}{(\sqrt{7} – \sqrt{6})}$
= $\cfrac{1}{(\sqrt{7} – \sqrt{6})}\times\cfrac{(\sqrt{7} + \sqrt{6})}{(\sqrt{7} + \sqrt{6})}$
= $\cfrac{(\sqrt{7} + \sqrt{6})}{(\sqrt{7})^2 – (\sqrt{6})^2}$
= $\cfrac{(\sqrt{7} + \sqrt{6})}{7-6}$
= $\cfrac{(\sqrt{7} + \sqrt{6})}{1}$
= $(\sqrt{7} + \sqrt{6})$
(iii) $\cfrac{1}{(\sqrt{5} + \sqrt{2})}$
= $\cfrac{1}{(\sqrt{5} + \sqrt{2})}\times\cfrac{(\sqrt{5} – \sqrt{2})}{(\sqrt{5} – \sqrt{2})}$
= $\cfrac{(\sqrt{5} – \sqrt{2})}{(\sqrt{5})^2 – (\sqrt{2})^2}$
= $\cfrac{(\sqrt{5} – \sqrt{2})}{5-2}$
= $\cfrac{(\sqrt{5} – \sqrt{2})}{3}$
(iv) $\cfrac{1}{(\sqrt{7} – 2)}$
= $\cfrac{1}{(\sqrt{7} – 2)}\times\cfrac{(\sqrt{7} + 2)}{(\sqrt{7} + 2)}$
= $\cfrac{(\sqrt{7} + 2)}{(\sqrt{7})^2 – (2)^2}$
= $\cfrac{(\sqrt{7} + 2)}{7 – 4}$
= $\cfrac{(\sqrt{7} + 2)}{3}$


