Q-1: Write the following in decimal form and say what kind of decimal expansion each has :
(i) $\cfrac{36}{100}$
(ii) $\cfrac{1}{11}$
(iii) $4\cfrac{1}{8}$
(iv) $\cfrac{3}{13}$
(v) $\cfrac{2}{11}$
(vi) $\cfrac{329}{400}$
Solution:
(i) $\cfrac{36}{100}$
$\cfrac{36}{100} = 0.36$
Decimal Expansion is terminating.
(ii) $\cfrac{1}{11}$
Performing long division, we get,
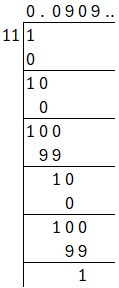
$\cfrac{1}{11} = 0.0909… = 0.\overline{09}$
Decimal expansion is non-terminating and repeating.
(iii) $4\cfrac{1}{8}$
$4\cfrac{1}{8} = \cfrac{33}{8}$
Performing long division, we get,
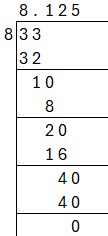
$4\cfrac{1}{8} = \cfrac{33}{8} = 8.125$
Decimal expansion is terminating.
(iv) $\cfrac{3}{13}$
Performing long division, we get,
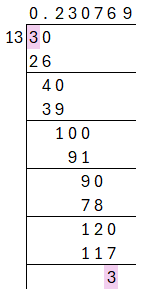
$\cfrac{3}{13} = 0.230769… = 0.\overline{230769}$
Decimal expansion is non-terminating and repeating.
(v) $\cfrac{2}{11}$
Performing long division, we get,
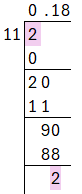
$\cfrac{2}{11} = 0.18… = 0.\overline{18}$
Decimal expansion is non-terminating and repeating.
(vi) $\cfrac{329}{400}$
Performing long division, we get,

$\cfrac{329}{400} = 0.8225 $
Decimal expansion is terminating.
Q-2: You know that $\cfrac{1}{7} = 0.\overline{142857}$ .
Can you predict what the decimal expansions of $\cfrac{2}{7} $, $\cfrac{3}{7} $ , $\cfrac{4}{7} $ , $\cfrac{5}{7} $ , $\cfrac{6}{7} $ are, without actually doing the long division? If so, how?
[Hint: Study the remainders while finding the value of $\cfrac{1}{7}$ carefully.]
Solution:
$\cfrac{1}{7} = 0.\overline{142857}$
$\therefore \cfrac{2}{7} = 2\times\cfrac{1}{7} =2\times 0.\overline{142857}= 0.\overline{285714}$
$\cfrac{3}{7} = 3\times\cfrac{1}{7} =3\times 0.\overline{142857}= 0.\overline{428571}$
$\cfrac{4}{7} = 4\times\cfrac{1}{7} =4\times 0.\overline{142857}= 0.\overline{571428}$
$\cfrac{5}{7} = 5\times\cfrac{1}{7} =5\times 0.\overline{142857}= 0.\overline{714285}$
$\cfrac{6}{7} = 6\times\cfrac{1}{7} =6\times 0.\overline{142857}= 0.\overline{857142}$
Q-3: Express the following in the form $\cfrac{p}{q}$, where p and q are integers and $q\ne0$.
(i) $0.\overline{6}$
(ii) $0.4\overline{7}$
(iii) $0.\overline{001}$
Solution:
(i) $0.\overline{6}$
Let $x = 0.6666….$ —————–(1)
Multiply both sides by 10, we get,
$10x = 6.6666….$
$\implies 10x = 6 + 0.6666…$
$\implies 10x = 6 + x$ (Using 1)
$\implies 10x – x = 6$
$\implies 9x = 6$
$\implies x = \cfrac{6}{9} = \cfrac{2}{3}$
$\therefore 0.\overline{6} = \cfrac{2}{3}$
(ii) $0.4\overline{7}$
Let $x = 0.4777….$ —————–(1)
Multiply both sides by 10, we get,
$10x = 4.7777….$ ——————(2)
Multiple both sides again by 10, we get,
$\implies 100x = 47.7777…$
$\implies 100x = 43 + 4.7777…..$
$\implies 100x = 43 + 10x$ (Using 2)
$\implies 100x -10x = 43$
$\implies 90x = 43$
$\implies x = \cfrac{43}{90}$
$\therefore 0.4\overline{7} = \cfrac{43}{90}$
(iii) $0.\overline{001}$
Let $x = 0.001001001….$ —————–(1)
Multiply both sides by 1000, we get,
$1000x = 1.001001….$
$\implies 1000x = 1 + 0.001001…$
$\implies 1000x = 1 + x$ (Using 1)
$\implies 1000x – x = 1$
$\implies 999x = 1$
$\implies x = \cfrac{1}{999}$
$\therefore 0.\overline{001} = \cfrac{1}{999}$
Q-4: Express 0.99999…. in the form $\cfrac{p}{q}$. Are you surprised by your answer? With your teacher and classmates discuss why the answer makes sense.
Solution:
Let $x = 0.9999….$ —————–(1)
Multiply both sides by 10, we get,
$10x = 9.999….$
$\implies 10x = 9 + 0.999…$
$\implies 10x = 9 + x$ (Using 1)
$\implies 10x – x = 9$
$\implies 9x = 9$
$\implies x = \cfrac{9}{9} = 1$
$0.9999999..$ or $0.\overline{9}$ is too close to 1. Therefore, we can consider it to be equal to 1.
Q-5: What can the maximum number of digits be in the repeating block of digits in the decimal expansion of $\cfrac{1}{17}$ ? Perform the division to check your answer.
Solution:
By using long division, we get,
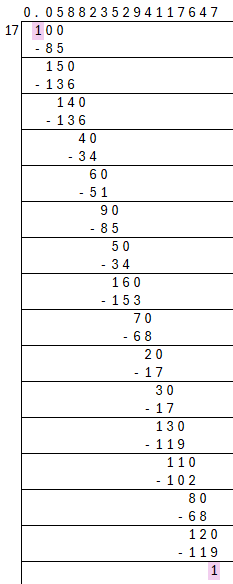
$\therefore \cfrac{1}{17} = 0 . \overline{0588235294117647}$ which means there are 16 digits in the repeating block.
Q-6: Look at several examples of rational numbers in the form $\cfrac{p}{q} (q \ne 0)$, where p and q are integers with no common factors other than 1 and having terminating decimal representations (expansions). Can you guess what property q must satisfy?
Solution:
Let’s consider few examples
$\cfrac{5}{2} = 2.5$————–terminating when denominator is 2 (or $2^1$)
$\cfrac{5}{4} = 1.25$————-terminating when denominator is 4 (or $2^2$)
$\cfrac{5}{8} = 0.625$————terminating when denominator is 8 (or $2^3$)
$\cfrac{2}{5} = 0.4$————–terminating when denominator is 5 (or $5^1$)
$\cfrac{2}{25} = 0.08$————terminating when denominator is 25 (or $5^2$)
$\cfrac{2}{200} = 0.01$———–terminating when denominator is 200 (or $2^3\times5^2$)
$\therefore$ We observe that the decimal expansion is terminating when the prime factorization of denominator has power of 2 or 5 or both.
Q-7: Write three numbers whose decimal expansions are non-terminating non-recurring.
Solution:
All irrational numbers are non-terminating non-recurring. three numbers with decimal expansions that are non-terminating and non-recurring are:
- $\sqrt{3} = 1.732050807568..$
- $\sqrt{26} = 5.099019513592..$
- $\sqrt{101} = 10.04987562112..$
Q-8: Find three different irrational numbers between the rational numbers $\cfrac{5}{7}$ and $\cfrac{9}{11}$.
Solution:

$\cfrac{5}{7} = 0.\overline{714285}$
$\cfrac{9}{11} = 0.\overline{81}$
Three different irrational number between $\cfrac{5}{7}$ and $\cfrac{9}{11}$ are
- 0.72072007200072…
- 0.731731173111731111…
- 0.752752275222752222…
Q-9: Classify the following numbers as rational or irrational according to their type:
(i) $\sqrt{23}$
(ii) $\sqrt{225}$
(iii) $0.3796$
(iv) $7.478478$
(v) $1.101001000100001…$
Solution:
(i) $\sqrt{23}$
$\sqrt{23}$ is an irrational number because it’s decimal expansion is non-terminating and non-recurring. [$\sqrt{23} = 4.79583152331…$]
(ii) $\sqrt{225}$
$\sqrt{225} = 15 = \cfrac{15}{1} $
$\therefore \sqrt{225}$ is a rational number because it can be expressed in form $\cfrac{p}{q}$.
(iii) $0.3796$
The number has a terminating decimal expansion therefore, it is a rational number.
(iv) $7.748748..$
The decimal expansion is non-terminating but recurring therefore, the number is rational.
(v) $1.101001000100001…$
The decimal expansion is non-terminating and non-recurring therefore, the number is irrational.


