Q-1: State whether the following statements are true or false. Justify your answers.
(i) Every irrational number is a real number.
(ii) Every point on the number line is of the form $\sqrt{m}$ where m is a natural number.
(iii) Every real number is an irrational number.
Solution:
(i) True
Irrational Numbers: A number is said to be irrational, if it cannot be written in the form $\cfrac{p}{q}$, where $p$ and $q$ are integers and $q\ne0$.
Real Numbers: The collection of both rational and irrational numbers is known as real numbers.
$\therefore$ Every irrational number is a real number, however, every real number is not an irrational number.
(ii) False
Negative number like $-3$ cannot be expressed in the form $\sqrt{m}$ where m is a natural number. Same is the case with all negative numbers.
(iii) False
Real numbers include both irrational and rational numbers.
$\therefore$ every real number cannot be an irrational number.
Q-2: Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is a rational number.
Solution:
We know,
$\sqrt{16} = 4$, which is not an irrational number.
Similarly, $\sqrt{25} = 5$, which is also not an irrational number
$\therefore$ the square roots of all positive integers are not irrational.
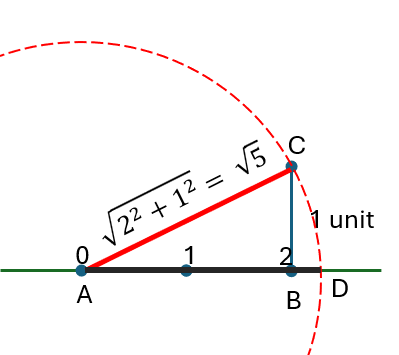
Q-3: Show how √5 can be represented on the number line.
Solution:
Draw line AB=2 unit
Apply pythagores theorem on $\triangle{ABC}$, $BC=\sqrt{AB^2+BC^2} = \sqrt{2^2+1^2} = \sqrt{5}$
Draw an arc with radius = BC = $\sqrt{5}$ intersecting the extended line AB at D where AD = $\sqrt{5}$
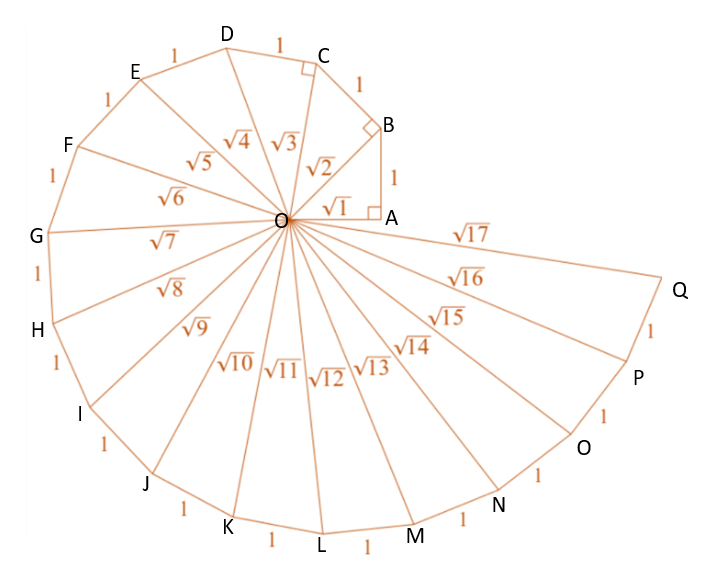
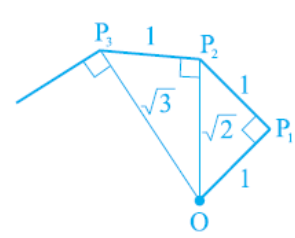
Q-4: Classroom activity (Constructing the ‘square rootspiral’) : Take a large sheet of paper and construct the ‘square root spiral’ in the following fashion. Start with a point O and draw a line segment $OP_1$ of unit length. Draw a line segment $P_1 P_2$ perpendicular to $OP_1$ of unit length (see Fig. 1.9). Now draw a line segment $P_2 P_3$ perpendicular to $OP_2$ . Then draw a line segment $P_3P_4$ perpendicular to $OP_3$. Continuing in this manner, you can get the line segment $P_{n–1}P_n$ by drawing a line segment of unit length perpendicular to $OP_{n–1}$. In this manner, you will have created the points $P_2, P_3,…., P_n,… .$, and joined them to create a beautiful spiral depicting $\sqrt{2},\sqrt{3},\sqrt{4}$….
Solution:
- Mark a point O on the paper. Here, O will be the center of the square root spiral.
- From O, draw a straight line, OA=1 unit horizontally.
- From A, draw a perpendicular line, AB =1 unit.
- Join OB. Here, OB = $\sqrt{1^2+1^2} = \sqrt{2}$
- Now, from B, draw a perpendicular line BC = 1 unit.
- Join OC. Here, OC = $\sqrt{(\sqrt{2})^2+1^2} = \sqrt{3}$
- Repeat the steps to draw $\sqrt{4}, \sqrt{5}, \sqrt{6}$….